Time is Money
“The Time Value of Money” and how to use it to make wiser investment decisions.
Table of Contents
2. Future Value
3. Present Value
4. Present Value & Discounting
5. Net Present Value
5. Internal Rate Return
6. Outro
The Time Value of Money
Let’s talk about it…
What’s it all about?
The time value of money is a core principle of finance and investment analysis. Understanding how to apply it is central to making wise investment decisions.
Understanding it (and more importantly knowing how to apply it) puts distance between you and your competitors that don’t.
It says that:
‘$1 today is worth more than $1 tomorrow’
Ok. Why?
Because a dollar today has the opportunity to earn a return between today and tomorrow. The dollar tomorrow has lost that opportunity, and can’t get it back.
Quick example.
Let’s say your buddy Jerry owes you $1. Today is Monday. He says he can drop it off today or Friday.
Now, let’s also say you have an investment vehicle available to you that earns you a daily return of 10%.
Nice.
Here’s how getting that dollar today vs Friday breaks down:
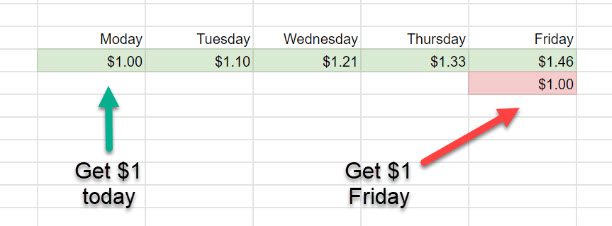
If he gives you that dollar today, and you invest it, come Friday you’ve got 46 extra cold hard cents melting a hole in your pocket. What you gonna spend it on, moneybags?
That dollar, received today, is worth $1.46 on Friday.
That same dollar, received on Friday, is just a dollar (worth $1.00).
Invested money can grow over time. Uninvested money atrophies over time.

(inflation compounds this atrophy issue even further)
Pretty simple right?
This Time-Value concept is most often expressed as the relationship between two values. The Present Value (PV) and the Future Value (FV) of an asset or cash flows.
Present Value ↔ Future Value
(or the relationship of a sum of money today and a sum of money down the road, and the impact they have on one another).
So how is this helpful? (Practically)
In a few ways.
It can help us answer a few important questions.
- How much will an investment made today be worth at some date in the future?
- How much would you need to invest now to reach a target amount in the future?
- How much is a future series of cash flows worth today? (Compared to your alternative investment options)?
- How profitable is an investment compared to alternatives?
- What is the return rate of a series of future cash flows?
Let’s get to it.
#1. How much will an investment made today be worth in the future?
(Future Value)
Let’s use a more practical example for this.
Say you’re interested in an investment property that offers a 10% annual rate of return. You expect it’s currently worth $1 MM. You’re weighing your options and are curious how much that investment will be worth 5 years from now.
We can determine this by solving for the Future Value (or FV) of the asset.
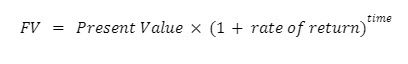
Now let’s plug in our numbers…
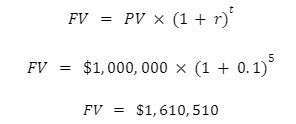
Five years from now, this $1 MM asset with 10% annual returns is worth $1,610, 510. That’s $610,510 more than today.
Use Future Value to determine how much your investment decisions today will be worth down the road.
Moving right along..
#2. How much do you need to invest (today) to reach a target amount in the future?
(Present Value)
Say you’ve set a personal investing goal for yourself:
“Five years from today, I want to have $500,000 in liquid assets.”
Next you ask yourself what you’ll need to do to achieve this goal.
To answer this, we can rearrange the future value formula from before, to solve for present value instead:
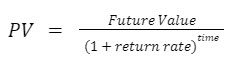
Before we can solve for present value (and answer how much we’ll need to invest to achieve our goal), we’ll need to answer another question first:
What investment vehicles do we have available to us? And of those, what is the highest rate of return?
Big Note: the highest rate of return doesn’t necessarily mean the best investment. Often higher returns mean higher risk. (Much more on that in a different write-up).
For this example, let’s use the same rate as last time (10% annual return). Great – now we have everything we need to solve for present value.
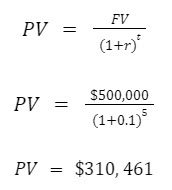
In order to achieve our goal of $500,000 in 5 years (with a 10% annual rate of return), we’ll need to invest $310,461 now.
Say that’s too much for us. We have some options.
Maybe we decide that 5 years is a little aggressive – $500,000 in 8 years from today should be just fine.
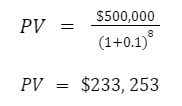
If we push our goal out to the 8 year mark, the investment required today is $233,253 ($77K less than necessary for 5 years).
Well maybe that’s still not good enough for us. We decide to go hunt for an investment with a better rate of return and we find one offering a 20% annual return. Let’s see how that shakes out.
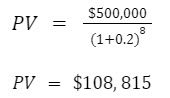
With this new investment vehicle (with a 20% annual return), investing $108,815 today will yield us $500,000 in 8 years.
You can see how powerful this can be for planning your investment strategy. And doing it with precision.
Alright. Time to take off the training wheels. On to the really fun stuff 🙂
* Cue Question 3 *
#3. How much is a stream of cash flows (in the future) worth to you today?
(Present Value)
Here’s where we really get to see the time value of money flex it’s power. And where we can start comparing investment options with more accuracy and precision.
So how do we value an investment?
And how do we do it within the context of our other investment options?
(No sense is tying up our money in a given subject investment if we have an alternative investment with higher returns and similar risk).
We do this by calculating the present value of our subject investment. And as part of that calculation we do something called discounting the future cash flows of the subject investment.
We learned earlier that the value of a dollar (or the value of a cash flow) down the road is less than the value of that same dollar (or a cash flow) today.
So when we’re considering how future cash flows (down the road) impact the value of the investment today, we have to discount (or reduce the value) of those future cash flows to accurately determine their value today.
($50,000 in 3 years is worth less than $50,000 today).
We know why…
Because the $50,000 today has the opportunity to earn a return across the next 3 years. Whereas the $50,000 in 3 years does not have that opportunity.
So we gotta discount it.
But how do we know how much to discount the $50,000 3 years from now?
We discount the value of those future cash flows by the return rate of our alternative investment option. (This rate is called the discount rate or the opportunity cost of capital). This is the rate of return that we’re foregoing, by investing in the subject investment as opposed to the alternative investment.
So our discount rate is the return rate of our next best investment option, with a similar risk profile.
The sum of all of the discounted cash flows that an investment offers is our present value.
By doing this, we can answer the question:
“How much is the subject investment worth to me today, considering its future cash flows and considering our other investment options?”
Now. If this is the first time you’re hearing about these concepts, I imagine the fog of confusion may be starting to set in.
Let’s look at an example to illustrate it a bit more clearly.
Let’s start by comparing two investments – Investment A and Investment B.
Investment A is old news to you. It yields a consistent 7% annual return. It’s reliable, it’s proven, and it’s available to you. (This will be our alternative investment)
Investment B is new. (This will be our subject investment). You have the opportunity to purchase a short-term rental investment that produces $60,000 annually in before-tax cash flow. The sellers are asking $300,000 for the property.
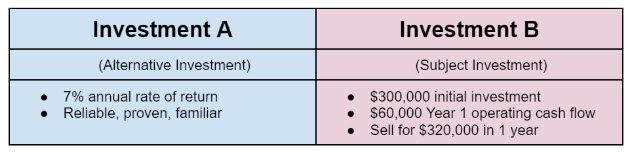
Now let’s determine what that investment would be worth to us.
Single Cash Flow Valuation
For the sake of simplicity, let’s first look at this considering only a single cash flow. Let’s say that we only want our capital tied up in this investment for a year.
We want to buy it, operate it for a year, receive the $60,000 in operating cash flow, and then sell it.
We’re confident that in a year we can sell it for at least $320,000.
So what is this opportunity worth to us? Or more specifically, what is the present value of this cash flow a year from now?
We’ll use the same present value formula as before:
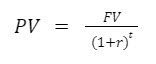
In this application, here’s how our inputs shake out:
- FV (future value): our future value in this case is the cash flow that we expect to receive 1 year from now. That’s the $60,000 in cash flow from operating the asset and the $320,000 from the sale of the asset. That makes for a future value of $380,000.
- r (rate of return): our rate of return in this case is our discount rate. We use the rate of return of our alternative investment option. (Remember, this is the return that we’re forfeiting by investing in the subject investment instead of the alternative investment). In our case, this is 7%.
- t (time or # of periods): since we’re looking at annual cash flow here and that cash flow occurs 1 year from today, our # of periods is 1.
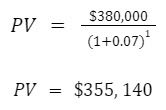
This subject investment, given our alternative investment options, is worth $355,140 to us today. Given that the asking price is $300,000 – this could be a great buy.
We walk into $55,150 of additional value.
Come on in, the water is fine.
(Now this example is made simple to highlight the concept. In real life we’d need to factor in the cost of acquisition, the cost of the sale, and debt service, fees, etc). Either way, the concept holds true.
Multiple Cash Flow Valuation
Now let’s take a look at the same subject investment, but given a more likely scenario. Specifically, we’re looking to hold it and operate it for more than a year. Let’s say 5.
Here we project the annual cash flows out for the next 5 years. In year 5, we’d like to sell and we’re confident that we can walk away with at least $388,000 in proceeds from that sale.
Here’s how that looks:

We have 5 different yearly cash flows to consider. How do we calculate the present value?
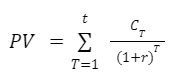
… or written another way …
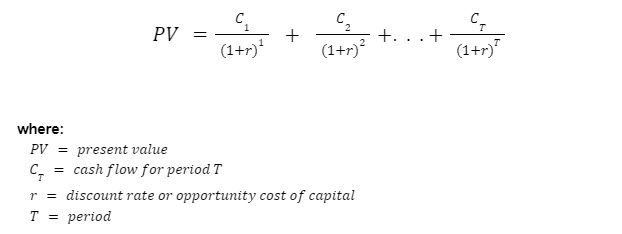
Now let’s plug our values in.
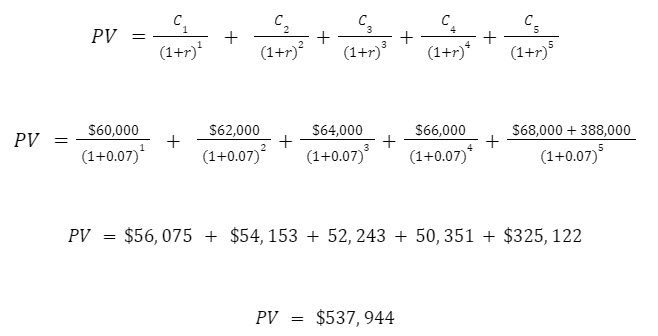
The present value of this investment’s cash flows across the next 5 years, given our alternative investment options, is $537,944.
This is a good buy for us.
This is well above the likely purchase price and well above the return that our alternative investment could produce. (And light years beyond how much that $300,000 would be worth if you stuffed it under your mattress)
Let’s have a quick look below.
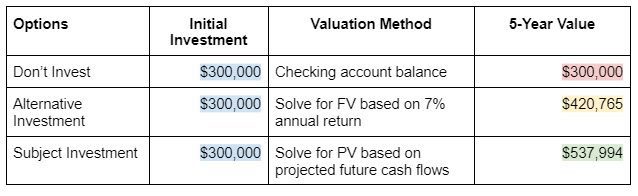
I think the winner is clear.

Use Present Value to determine how much an investment is worth to you!
Now . . . How can we determine how profitable an investment is?
* NPV enters stage left *
#4. How profitable is an investment, compared to alternatives?
(Net Present Value)
That’s right people. We’re talking Net Present Value aka NPV.
Net Present Value is a useful metric that goes a step beyond “how much is this investment worth to me” and answers the questions “how much profit does this investment stand to generate for me?”
Once you have a grasp on the concept of Present Value, understanding Net Present Value is pretty simple. Here’s the important distinctions:
- Present Value looks at all future cash flows (positive or negative), but does not consider the initial investment made (negative cash flow) to buy-in to the investment
- (which tells you how much a stream of future cash flows is worth today)
- Net Present Value does factor in this initial buy-in at time zero.
- (which tells you how much profit a stream of future cash flows will generate)
Simply put:
Less simply put (though this should look familiar now):
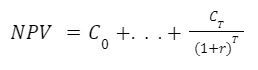
So in the case of our subject investment option from above:
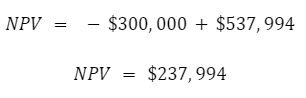
By electing to invest, we stand to profit $297,994 more than we otherwise would have across the next 5 years.
Pretty useful right?
Now, Net Present Value can be positive or negative.
- If NPV is negative, the investment is not profitable. You will lose money.
- If NPV is zero, you break even.
- If NPV is positive, the investment is profitable. You make money.
“The NPV Rule” is an idea that suggests that investors should pursue opportunities / projects that have a positive net present value.
And if you have multiple options available to you with a positive NPV, but you can only pursue a subset, you should select the project(s) with the highest NPV.
#5. What’s the return rate of a stream of future cash flows?
(Internal Rate of Return)
Home stretch. Last question.
This time, let’s start with the example. Take our subject investment from before. Here are our knowns:
- We know what we can buy it for ($300,000)
- We’ve projected is operating cash flows across the next 5 years (starting at $60K)
- We’re confident that we can sell it for $388,000 5 years from now
But what is the actual rate of return of this project?
We can answer this by solving for another profitability metric called Internal Rate of Return or IRR.
IRR measures the intrinsic profitability of an investment. It is the rate of return that you obtain by investing in a given project.
Where PV and NPV consider that value of an investment compared to alternative, IRR looks only at the Internal profitability of the subject investment.
The beauty of this is if we know the IRR of our alternative investment options (which we do) and we know the IRR of our subject investment (which we don’t yet). We can quickly make a judgment call on which is better (so long as they both have a similar risk profile).
We know that our alternative investment from before has a 7% annual IRR. Now back to our original question:
What is the IRR of our subject investment?
Internal Rate of Return is the Discount Rate of an investment at which the Net Present Value is equal to zero. It represents the true earnings of an investment.
Here’s that same statement expressed formulaically:
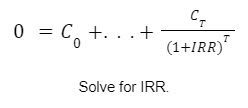
(I can sense minds smoking)
Now in practice you’ll be able to determine IRR much more easily than loading that formula up with all of your cash flow information and solving for IRR.
(In fact in most real work examples solving for IRR by hand would be a massive waste of time bordering on nearly impossible)
Most if not all software used for financial modeling comes with IRR functions out of the box to do the calculations for you. So use those instead of attempting by hand 🙂
What’s more important than the underlying math is understanding the concept and how to apply it.
Speaking of applying it, let’s calculate the IRR for our subject investment.
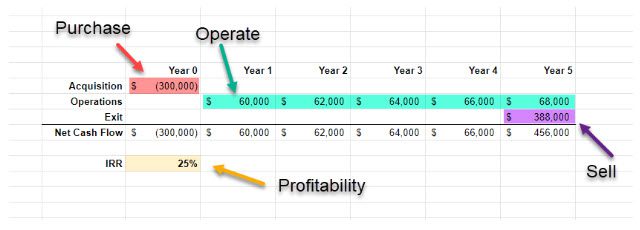
The internal rate of return of our subject investment is 25%.
Armed with this information, we can more quickly answer the question “should we move on the subject investment (25% IRR) or our alternative investment (7% IRR).
(The subject investment is the clear winner)
Generally speaking, “The IRR Rule” states that if the IRR of a project is higher than your opportunity cost of capital (i.e. the return rate of your alternative investment) – it is worth pursuing.
Practically speaking though, there’s more context needed to make the “Invest in A, not B” decisions.
If you come across a scenario where “The NPV Rule” and “The IRR Rule” are giving you competing recommendations, it is generally wiser to follow “The NPV Rule” recommendation.
Wrapping Up
We’ve covered a lot.
We outlined the core investment principle “The Time Value of Money”.
We answered five common investing questions:
- How much will an investment made today be worth at some date in the future?
- How much would you need to invest now to reach a target amount in the future?
- How much is a future series of cash flows worth today? (Compared to your alternative investment options)?
- How profitable is an investment compared to alternatives?
- What is the return rate of a series of future cash flows?
And we learned how to deploy four of the most common time value metrics to determine value and profitability of potential investments:
- Future Value
- Present Value
- Net Present Value
- Internal Rate of Return
As you can imagine, what we covered just scratches the surface of investment / financial modeling. Though these concepts are the core of understanding how to turn money today into more money tomorrow.
And a thorough understanding of them puts you miles ahead of others in the market who don’t.
A man by the name Warren Edward Buffet (the founder of a modest holdings company in Omaha, Nebraska) outlined a few investing rules that he attributes much of his success to. The first two are pertinent here:

What we covered above arms you with some powerful tools to make sure you don’t.
Happy hunting 🙂
And if you’d rather I do the hunting for you, click here to let me know.
Learn More
This is only one of our many resources, if you enjoyed this you should check out the rest!



